Pressure is one of the most frequently measured and controlled physical measurands in automation technology. It has a direct influence on the flow of production and industrial processes. This article explains the basics of pressure and its measurement.
The pressure p is defined as the quotient of the magnitude of the force F and the size of the area A.
The force is distributed vertically over the entire surface.
The SI unit for pressure is the pascal (Pa).
1 Pa=N/m²
The force F always has a direction (here: vertical) and is therefore a vector. The pressure p, on the other hand, has no direction - it is a scalar. Within a closed system, e.g. a pressure reservoir, the pressure always acts perpendicularly on all surfaces equally. In practice, this means that the mounting position of the pressure transmitter or diaphragm can be chosen arbitrarily. For example, the pressure in the accumulator of a compressor can be measured by mounting the pressure transmitter on the top of the tank, with the diaphragm pointing downwards.
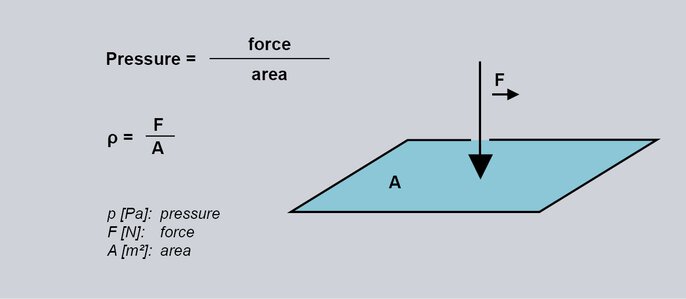
Fig. 1: Definition of pressure
If a surface of 1 m2 is loaded with 100 g of weight force (F = 0.1 kg × 10 m/s2 = 1 N), this results in a pressure of 1 Pa.* The unit commonly used in Europe for higher pressures is Bar (bar). As can be seen in the calculation, Pascal (Pa) has too small a division for most technical applications.
1 bar = 105 N/m² = 100 000 Pa
The unit bar (bar) is usually found on the measuring scale of pressure gauges or process variable recorders. It is interesting to note that mmHg (millimeters of mercury) is a unit frequently used in medicine. This is used to determine systolic blood pressure.
1 mmHg = 133,322 Pa
According to the definition, if a force of gravity F = 1N (1N is the product of the mass m = 100 g and the acceleration due to gravity g = 10m/s2) acts on a given area A = 1 m2 , the pressure is 1 Pa.
Pressure formula and unit:
p = F/S, where:
p - Pressure [Pa]
F - Power [N]
S - Surface [m2].
You can use the above formula to calculate the pressure if you know the mass of the object or medium to be tested. But what if you need to calculate the pressure at the bottom of a large container, such as a swimming pool? In this case, it is impossible to determine the total mass of the water. Using a formula, it is possible to determine the pressure at the bottom of the container based solely on the density and height of the column of the medium:
Pressure formula:
p = ρgh +p0, where:
ρ - Medium density [kg/m3]
g - Acceleration due to gravity [m/s2].
h - Liquid column height [m].
*Note: The exact value of the acceleration due to gravity g = 9.81 m/s2 was not used here. Instead, a rounded value of 10 m/s2 was used.
The zero point of the absolute or absolute pressure scale is the vacuum. Therefore, absolute pressure data is always measured with respect to it. An example is atmospheric pressure, which is always reported as absolute pressure..
When measuring the
relative pressure, the reference value is the ambient pressure value. In industrial applications, the pressure in equipment is often specified in relative form, i.e. in relation to atmospheric pressure. In this case, the actual pressure is the sum of the relative pressure (as it occurs in the process) and the ambient pressure (atmospheric). In industry, however, it is not uncommon for processes to occur at pressures that are many times the atmospheric pressure. In such cases, the ambient pressure is not taken into account.
Static pressure is the pressure in a gas or liquid at rest, e.g. in a closed vessel. In this case, it is sufficient to know the force exerted by the medium on a given surface to determine the pressure. However, if the medium is in motion, e.g. in a pipeline, it is referred to as dynamic pressure. By definition, dynamic pressure can be described as the pressure exerted by a flowing liquid or gas on the surface of a body at right angles to the flowing medium. This pressure results from the kinetic energy of the moving particles.
Differential pressure is the result of comparing two absolute pressure values and is referred to as the pressure difference Δp. It is often used in engineering applications for control purposes. For example, the difference in pressure at the bottom of a liquid container and above the liquid provides information about the height of the liquid column. A differential pressure gauge, such as a differential pressure transmitter, makes pressure measurements at two measuring points.
Hydrostatic pressure occurs in a fluid at rest. It depends on the height of the liquid column h, its density ρ and the acceleration due to gravity g. The higher the water column, the higher the pressure. The deeper a diver dives in a lake, for example, the greater the hydrostatic pressure acting on him.
